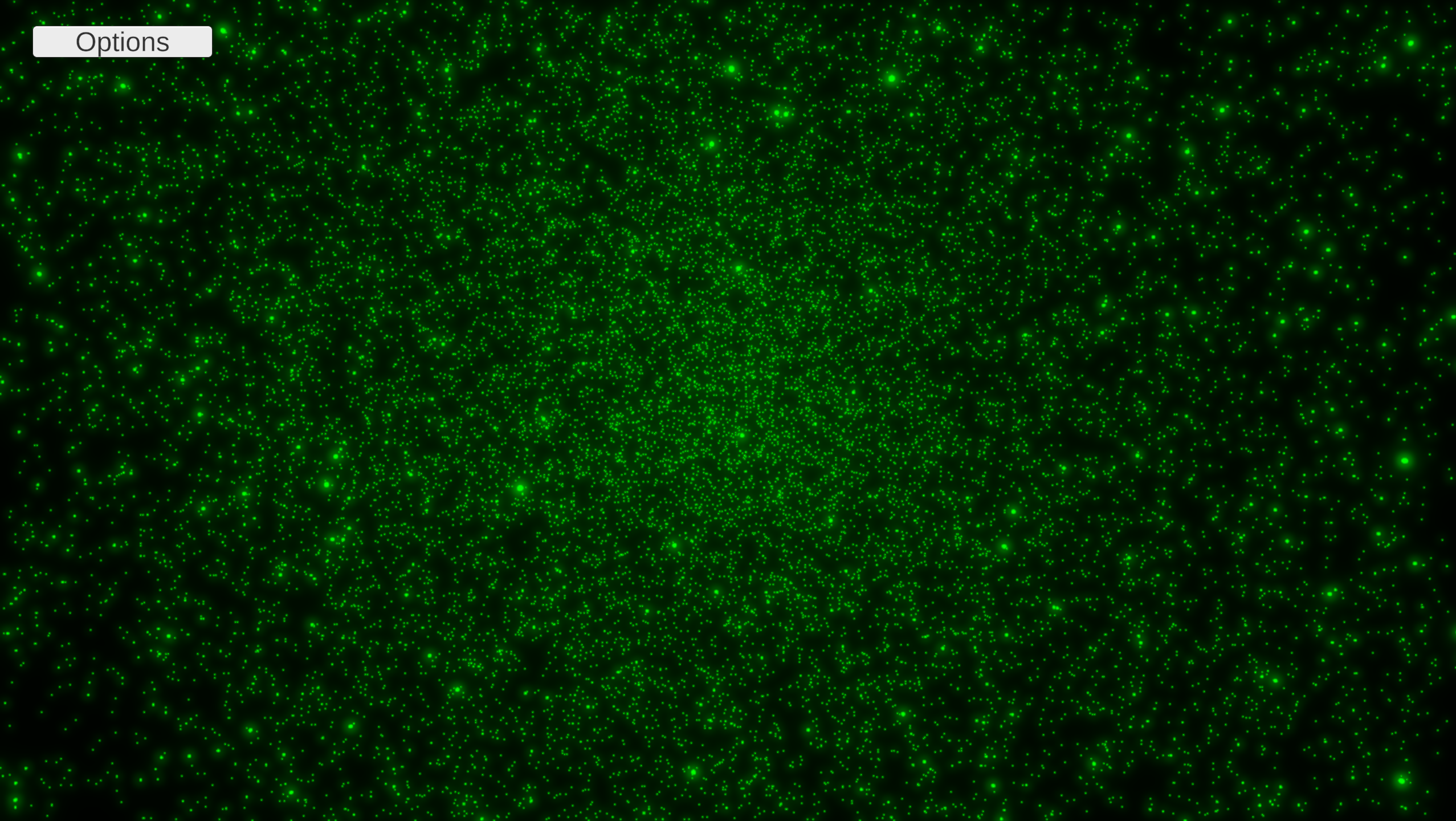
N-Body Gravitational Modeler

1. Project Overview & Core Concept

This project is a high-performance, interactive prototype built in Unity that simulates the gravitational dynamics of an N-body system.

The Core Idea

The “N-body problem” is a classic computational challenge: how do you simulate the motion of $N$ (e.g., 100,000) particles that are all gravitationally attracting each other?

A simple, “brute-force” approach, where every particle calculates the force from every other particle, is an O(n^2) algorithm. This means for 100,000 bodies, you would need 100,000 times 100,000 = 10,000,000,000 (ten billion) calculations per frame, making real-time simulation impossible.

This prototype solves this performance barrier by implementing a dual optimization strategy:

1. Algorithmic Optimization: It uses the Barnes-Hut algorithm, an O(n \log n) approximation that intelligently groups distant particles into clusters, drastically reducing the number of calculations.

2. Hardware Optimization: It leverages Unity’s Data-Oriented Technology Stack (DOTS), specifically the C# Job System and Burst Compiler, to execute all simulation logic in parallel across all available CPU cores.

The result is a fully custom physics sandbox, running its own simulation logic completely independent of Unity’s built-in 3D physics engine. It is capable of handling hundreds of thousands of bodies in real-time while providing a full UI to control the simulation’s physical parameters.

2. Technical Explanation

The simulation’s architecture is managed entirely by nBodyManager.cs, which schedules a chain of jobs every frame.

The Algorithm: Barnes-Hut

The Barnes-Hut algorithm is implemented in three main phases, each as its own job:

1. Octree Construction (buildOctreeJob.cs) An Octree is a 3D tree structure that recursively subdivides space into 8 cubes (octants). Every frame, buildOctreeJob.cs builds a new tree and inserts all particles into it. The Insert function [cite: buildOctreeJob.cs] recursively finds the correct node for a particle. If a leaf node is already full, it “subdivides” by creating 8 new children and re-inserting both particles.

// From buildOctreeJob.cs
private void Insert(int nodeIndex, int bodyIndex, int depth)
{
    octreeNode node = octree[nodeIndex];
    if (!node.IsLeaf) // If internal node, find the correct child
    {
        int childIndex = GetChildOctant(node, bodies[bodyIndex].position);
        Insert(node.firstChildIndex + childIndex, bodyIndex, depth + 1);
        return;
    }
    
    if (node.particleIndex == -1) // If leaf is empty
    {
        node.particleIndex = bodyIndex;
        octree[nodeIndex] = node;
        return;
    }
    
    if (depth < maxDepth) // If leaf is full, subdivide
    {
        // ... (code to create 8 children) ...
    }
}

2. Center of Mass (calcCenterOfMassJob.cs) Once the tree is built, this job walks the tree from the bottom-up (leaves to root). Each parent node calculates its own totalMass and centerOfMass based on the sum and weighted average of its children [cite: calcCenterOfMassJob.cs].

// From calcCenterOfMassJob.cs
private float CalculateMassRecursive(int nodeIndex)
{
    octreeNode node = octree[nodeIndex];
    if (node.IsLeaf)
    {
        // ... (get mass from single particle) ...
        return node.totalMass;
    }
    
    float totalMass = 0;
    float3 weightedPositionSum = float3.zero;

    for (int i = 0; i < 8; i++) // Loop through 8 children
    {
        int childIndex = node.firstChildIndex + i;
        float childMass = CalculateMassRecursive(childIndex);
        if (childMass > 0)
        {
            totalMass += childMass;
            weightedPositionSum += octree[childIndex].centerOfMass * childMass;
        }
    }
    node.totalMass = totalMass;
    node.centerOfMass = weightedPositionSum / totalMass;
    // ...
    return totalMass;
}

3. Force Calculation (barnesHutForceJob.cs) This is the core of the algorithm. For every particle, this job traverses the Octree from the root. For each node it encounters, it runs the Theta ($\theta$) Criterion [cite: barnesHutForceJob.cs]:

// From barnesHutForceJob.cs
float d = math.distance(myBody.position, node.centerOfMass);
float s = node.size;

if ((s / d) < theta && !node.IsLeaf)
{
    // CASE 1: Node is "Far Away". Approximate as one particle.
    myForce += CalculateForce(myBody, node.centerOfMass, node.totalMass, d);
}
else
{
    // CASE 2: Node is "Too Close" or is a Leaf. Investigate further.
    if (node.IsLeaf && node.particleIndex != -1)
    {
        // ... (calculate force from the single particle) ...
    }
    else if (!node.IsLeaf)
    {
        // ... (push all 8 children to the stack to check them next) ...
    }
}

Multithreading: The C# Job System

The nBodyManager.cs script schedules this 5-step process every FixedUpdate [cite: nBodyManager.cs, FixedUpdate()]:

// From nBodyManager.cs - FixedUpdate()

// 1. Build the tree (single-core)
var buildTreeJob = new buildOctreeJob { ... };
JobHandle treeHandle = buildTreeJob.Schedule();

// 2. Calculate mass (single-core, depends on tree)
var comJob = new calcCenterOfMassJob { ... };
JobHandle comHandle = comJob.Schedule(treeHandle);

// 3. Main Thread Sync Point
comHandle.Complete();

// 4. Calculate forces (multi-core, uses data from sync)
var forceJob = new barnesHutForceJob
{
    octree = m_OctreeList.AsArray(), // Safe to read now
    ...
};
JobHandle forceHandle = forceJob.Schedule(numberOfBodies, 32);

// 5. Apply physics (multi-core, depends on forces)
var applyForcesJob = new applyForcesJob { ... };
JobHandle applyForcesHandle = applyForcesJob.Schedule(numberOfBodies, 32, forceHandle);

m_SimulationHandle = applyForcesHandle;

All jobs are marked with [BurstCompile], which translates them into highly optimized machine code, providing C++ like performance from C#.

Custom Physics & Rendering

• Custom Collisions: A “penalty force” system is built directly into barnesHutForceJob.cs. When the Octree traversal finds two “leaf” particles that are overlapping, it applies a simple, spring-like repulsive force [cite: barnesHutForceJob.cs]:

  // From barnesHutForceJob.cs
  if (d < radiusSum) // If particles are overlapping
  {
      float overlap = radiusSum - d;
      float3 direction = (myBody.position - otherBody.position) / d;
      // Add a spring-like penalty force
      myForce += direction * overlap * collisionStiffness;
  }
      
  

• High-Performance Rendering: To render 100,000+ objects, nBodyManager.cs bypasses GameObjects. In LateUpdate, it copies all particle positions into a Matrix4x4 array and uses Graphics.DrawMeshInstanced to render all of them in a single, efficient draw call [cite: nBodyManager.cs, LateUpdate()].

  // From nBodyManager.cs - LateUpdate()
  for (int i = 0; i < numberOfBodies; i++)
  {
      m_Matrices[i].SetTRS(m_Bodies[i].position, Quaternion.identity, Vector3.one);
  }
      
  Graphics.DrawMeshInstanced(
      particleMesh,
      0,
      particleMaterial,
      m_Matrices,
      numberOfBodies,
      m_Props
  );
      
  

3. Showcase & User Guide

How to play?

Github repository link

• Go to the releases tab

• Click on the N-body.Gravitational.Modeler.Prototype.Windows.zip (<–or you may just click the link here <–)

• Unzip the file and click on the “N-Body Gravitational Modeler Prototype.exe” file to open the game.

• done, press Alt+Tab if you would like to stop the game.

Youtube Showcase link

How It Works

The simulation is a self-contained physics sandbox. The camera can be controlled via the mouse, and all simulation parameters are live-editable in the UI.

• Camera Controls (orbitCamera.cs):

  • Hold Left-Click & Drag: Orbit the camera around the center.

  • Hold Middle-Click & Drag: Pan the camera target.

  • Mouse Wheel: Zoom in and out.

  • Note: The camera intelligently stops moving if the mouse is over the UI panel (EventSystem.current.IsPointerOverGameObject()) [cite: orbitCamera.cs], allowing you to use sliders without moving the camera.

• Menu Controls:

  • Menu Button: Toggles the visibility of the control panel (ToggleMenu()).

  • Restart Simulation Button: This button is required to apply changes to Number of Bodies or Spawn Radius. It destroys the current simulation, disposes all memory (CleanupSimulation()), and creates a new simulation with the new parameters (InitializeSimulation())

Slider Guide

Simulation Controls (Require Restart)

• Number of Bodies (Input): Sets the number of particles to create.

• Spawn Radius (Input): Sets the radius of the sphere in which particles are initially spawned.

Real-Time Parameters (Live Update)

• Gravity: Controls the gravitationalConstant G. Higher values create a stronger pull, causing the simulation to form clusters and collapse faster.

• Stability (Softening): Controls the softeningFactor. This is a crucial numerical stability parameter that prevents the gravity equation from exploding to infinity when two particles get too close.

  • Low Value: More accurate, “point-like” gravity, but unstable. Prone to explosions.

  • High Value: More stable, but “mushy” physics, as forces are weakened at close range.

• Accuracy (Theta): Controls the theta value for the Barnes-Hut algorithm. This is the Speed vs. Accuracy slider.

  • Low Value (e.g., 0.2): High accuracy. The simulation performs more calculations.

  • High Value (e.g., 1.5): Low accuracy. The simulation is much faster but may be “lumpy” or inaccurate.

• Collision Stiffness: Controls the collisionStiffness value. This is the strength of the custom “penalty force” collision. When two particles overlap, this value determines the strength of the spring-like force pushing them apart.

• Color (R, G, B): Sets the base color of all particles.

• Lumination: Acts as a brightness/emission multiplier for the base color, creating an HDR effect for the particles.

Visual showcase